All of these are rather abstract things for a physics student as I rarely have a skyscraper or battlecruiser handy, and to me wind blows in straight lines. When was the last time you read "the icy wind was blowing from the north with a radius of curvature of 50km"? If I had a fully-crewed battlecruiser I would do nothing else but try to hit shipping at all possible latitudes in both hemispheres, but sadly I don't.
All of these examples are of the coriolis effect because of the earth's rotation. Things are much more fun and managable on smaller things which rotate every few seconds rather than planets which rotate once a day, such as roundabouts in this YouTube clip.
Last week I experienced my first ever difficulties with the Coriolis force. I was trying to turn around whilst juggling 5 balls, and found that if I turned clockwise then my right hand was catching balls far from the body and my left hand was catching them close to the chest. If I turned the other way then exactly the opposite happened. Was this the Coriolis force? Having read so many phenomena which are attributed to the Coriolis force but which aren't I thought I'd better check this out to make sure that it wasn't just bad aiming because of dizziness.
If you throw a ball from one hand to the other so that it stays in the air for one second, and your hands are half a metre apart, then the horizontal speed (v) is 0.5m/s. If you turn around every 12 seconds then you will have an angular velocity (omega) of about 0.5 rad/s.
The size of the coriolis acceleration is 2*omega*v, so to you the ball will appear to be accelerated inwards or outwards at about 0.5 m/s^2, which is about 1/20th of g, the acceleration due to gravity. The ball will land about 25cm further away (or closer to you) than you would expect. Maybe I wasn't turning that fast, because this seems a bit too much, but it's not far off what I was doing.
The centrifugal force depends on the square of omega, so it's not too important for slow rotations. Of course for fast rotations it quickly becomes important, see here, here and here.
Having had a few minutes of enjoyment (and then dizziness) experiencing this elusive force first hand I found that I'd got the hang of juggling whilst turning, and was automatically correcting for it quite nicely. It was fun while it lasted.
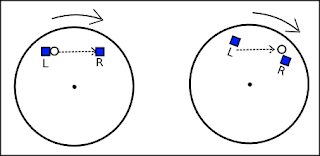
It took me a long time to understand why, if your throw an object in the direction of rotation, it should appear to move away from you or towards you. I only really got it whilst drawing the following diagram. Those blue squares represent a pair of hands, the small round thing is a ball, which starts from the left hand and is aimed at the right one. During the flight the hands rotate around the point in the middle, and if you're in control of the hands then the ball appears to make a curve. Of course somebody hovering above you would argue that your hands were curving and not the ball.
No comments:
Post a Comment